Sponsored Link
Install webmin on ubuntu 11.04 (Natty) server
We have already discussed how to install ubuntu 11.04 LAMP server now we will install webmin for easy administartion
Edit /etc/apt/sources.list file
sudo vi /etc/apt/sources.list
Add the following lines
deb http://download.webmin.com/download/repository sarge contrib
deb http://webmin.mirror.somersettechsolutions.co.uk/repository sarge contrib
Save and exit the file
Now you need to import GPG key
wget http://www.webmin.com/jcameron-key.asc
sudo apt-key add jcameron-key.asc
Update the source list
sudo apt-get update
Install webmin
sudo apt-get install webmin
Now you need to access webmin using http://serverip:10000/ once it opens you should see similar to the following screen
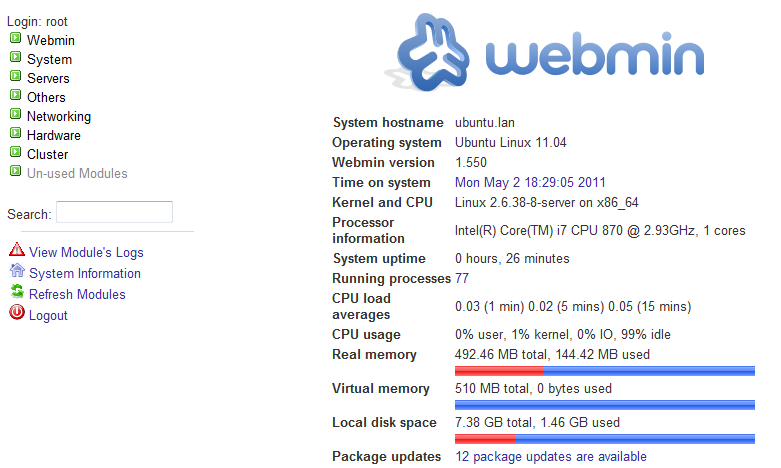
You need to eneter root username and password to login.Once you logged in you should see similar to the following screen



The repository is for Sarge, which is quite old. Can webmin manage to configure different versions of apache, samba, … ? I supose there has been some changes between sarge and 11.04.
Thank you.
+1 to Vincente,
it seems alot of the config paths are off, it would be nice to see an update
For some reason for which i do not now every time I install webmin correctly I can not log as root or with my admin account on my ubuntu 11.04 server. Can you help me with this please.
Shemaiah – u need to create a pwd for root. Then you can use root as a login and pass (for webmin)
After following the instructions from this guide when I go to log into webmin I get this error -bash https://ubuntu:10000/ no file or directory exists. Not sure what I am missing. that url is the one provided when Webmin finishes installing.
try it with http://:10000 , not https
try with this
https://serveripaddress:10000
Tried all both of those and still getting the same error.
did you run:
/etc/init.d/webmin start
That may fix it, you can also restart it with
/etc/init.d/webmin restart
Thanks that helped
What username and password do i need? I’ve tried with the user/pwd i’ve made the server installation and it did’t work. Got an login error. Thanks.
To fix password problem:
http://www.webmin.com/faq.html
* How do I change my Webmin password if I can’t login?
Included with the Webmin distribution is a program called changepass.pl to solve erecisely this problem. Assuming you have installed Webmin in /usr/libexec/webmin, you could change the password of the admin user to foo by running
/usr/libexec/webmin/changepass.pl /etc/webmin admin foo
changepass.pl is not included in the sarge deb as far as I can tell.
I’m also stuck at the login. I reversed hased the default md5 hash and it was ‘test’. That didn’t work.
So I can get to it by http://ipaddess:10000 but can’t log in…
@mike:
>changepass.pl is not included in the sarge deb as far as I can tell.
It is ‘cos I’ve just had to do the same 🙂
sudo /usr/share/webmin/changepass.pl /etc/webmin root yournewpasword
Hello all,
i have read this helpful thread on openserve.eu, this solved my problem with Webmin login.
– sudo find / -name changepass.pl
(normal path /usr/share/webmin)
– cd /usr/share/webmin
– sudo find / -name miniserv.conf
(normal path /etc/webmin/)
– sudo ./changepass.pl /etc/webmin/ root typeyourpasswordhere
this was very helpful for me. I can use my Webmin normal.
greats
Thank you very much for your How To ! I followed your instructions for an Ubuntu 8.04 server and it worked ! Now I have the latest version (1.550) of Webmin.
New Error from todays install using your instructions: /etc/apt# sudo apt-get install webmin
Reading package lists… Done
Building dependency tree
Reading state information… Done
Some packages could not be installed. This may mean that you have
requested an impossible situation or if you are using the unstable
distribution that some required packages have not yet been created
or been moved out of Incoming.
The following information may help to resolve the situation:
The following packages have unmet dependencies:
webmin : Depends: libnet-ssleay-perl but it is not installable
Depends: libauthen-pam-perl but it is not installable
Depends: apt-show-versions but it is not installable
E: Broken packages
I follow the instructions and get
sudo apt-get install webmin
Reading package lists… Done
Building dependency tree
Reading state information… Done
webmin is already the newest version.
You might want to run ‘apt-get -f install’ to correct these:
The following packages have unmet dependencies.
webmin : Depends: libnet-ssleay-perl but it is not going to be installed
Depends: libauthen-pam-perl but it is not going to be installed
Depends: libio-pty-perl but it is not going to be installed
Depends: apt-show-versions but it is not going to be installed
E: Unmet dependencies. Try ‘apt-get -f install’ with no packages (or specify a solution).
:~$ ps -ef | grep webmin
dub 2845 1260 0 14:29 pts/0 00:00:00 grep –color=auto webmin
What have i missed?
Hi.
I resolved the user login problem on Ubuntu 11 by editing /etc/webmin/miniserv.users and adding my username in there, and I didn’t have to change the root password.
Hope that help someone.
Thanks to everyone but especially ronny!
I follow the instructions and get too
sudo apt-get install webmin
Reading package lists… Done
Building dependency tree
Reading state information… Done
webmin is already the newest version.
You might want to run ‘apt-get -f install’ to correct these:
The following packages have unmet dependencies.
webmin : Depends: libnet-ssleay-perl but it is not going to be installed
Depends: libauthen-pam-perl but it is not going to be installed
Depends: libio-pty-perl but it is not going to be installed
Depends: apt-show-versions but it is not going to be installed
E: Unmet dependencies. Try ‘apt-get -f install’ with no packages (or specify a solution).
Could anyone help please?
Please help I have complyted the instaliation but I cant login to webmin. Google chrome and Explorer
cant find http://ubuntu:10000/ Anybody have some ideas?? pls.
Thanks everybody
Try to use the following format
https://your-server-ip:10000
Note:- where your-server-ip is 192.168.x.x or 172.x.x.x
sudo apt-get install webmin
After this i am getting the error message E:Unable to locate package webmin
sudo apt-get -f install
Reading package lists….Done
Building dependency tree
Reading state information…Done
0 upgraded, 0 newly installed, 0 to remove and 57 not upgraded
This is what the message i get
I am unable to login to webmin
I did the bellow mentioned thing
sudo apt-get -f install
Reading package lists….Done
Building dependency tree
Reading state information…Done
0 upgraded, 0 newly installed, 0 to remove and 57 not upgraded
This is what the message i get