Sponsored Link
The tutorial is pretty long due to the images, but they explain things easier sometimes (they are not just meaningless screenshots) (forgive me for your scroll button :P)
I tested this on Windows Xp, using my Ubuntu Linux's root partition for test purposes and everything went ok, but be aware:
Warning
Raw hard disk access is for expert users only. Incorrect use or use of an outdated configuration can lead to total loss of data on the physical disk. Most importantly, do not attempt to boot the partition with the currently running host operating system in a guest. This will lead to severe data corruption.
as stated in the VirtualBox manual!
download and install sun virtualbox for windows
(http://www.virtualbox.org/wiki/Downloads)
download the 32-bit ubuntu server edition
(http://www.ubuntu.com/getubuntu/download-server)
open up a windows command prompt (Start Menu > All programs > Accessories)
change into to the sun virtualbox folder:
cd "C:\Program Files\Sun\VirtualBox"
(tailor this if you have a non-standard Windows or VirtualBox installation)
find your ext3 partition:
VBoxManage internalcommands listpartitions -rawdisk \\.\PhysicalDriveX
(where X should be 0,1,... depending on which hdd you want to use)
(tip: ext3 partition type is 0x83)
create a special image which points to your partition:
VBoxManage internalcommands createrawvmdk -filename \path\to\file.vmdk -rawdisk \\.\PhysicalDriveX -partitions Y,Z
(where Y, Z should be the partition number(s) you found out before, and filename is self-explanatory, but should end with .vmdk)
set up a virtual machine in virtualbox:
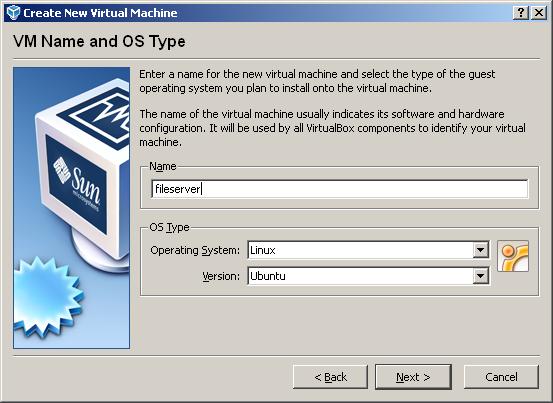
select your virtual machine and click on settings:
set up networking:
"insert" your ubuntu server install cd into the virtual machine:
start up your virtual machine and install ubuntu server:
select your keymap, and select the install mode:
the install is pretty self explanatory, you shouldn't have problems with it
choose samba file server and openssh server when asked
unmount the install medium and boot into your new system
update your system (optional), install some additional stuff(required):
sudo apt-get update (optional)
sudo apt-get dist-upgrade (optional)
sudo apt-get install screen nano mc htop
screen > allows multiple terminals to be opened easily
nano > easier to use than vim in my opinion
mc > just like norton commander or total commander
htop > easy process management
stop your virtualmachine and add the physical patrtition‘s image to the virtual machine
(image should be added to available images in virtual device manager first)
boot up your server again
make a new directory for the shared partition
cd /
mkdir sharedpartition
chmod 777 sharedpartition
edit your fstab to auto-mount the partition at every startup:
sudo nano /etc/fstab
add the following
/dev/sdXY /sharedpartition ext3 relatime,errors=remount-ro 0 1
(where X should be a,b,... depending on hdd number, and Y should 1,2,... depending on partition number)
edit samba configuration:
sudo nano /etc/samba/smb.conf
change your workgroup to be the same as your windows one, and uncomment the security line:
workgroup = yourworkgroup
security = user
add this to the end:
[SharedPartition]
comment = The shared physical partition
path = /sharedpartition
browseable = yes
writeable = yes
valid users = tutorial
now add and enable this user to samba
sudo smbpasswd -a tutorial
sudo smbpasswd -e tutorial
restart samba with
sudo /etc/init.d/samba restart
Enjoy!
P.s:
You can share multiple partitions and/or different filesystems too.


Or use ext2fsd ! works fine whit ext3 !
Aren’t there drivers for this?
Seriously?
Isn’t that just a little bit like taking a sledgehammer to crack a nut?
Alternatives:
http://www.diskinternals.com/linux-reader/
http://www.fs-driver.org/
Or, instead of this overtly long and complicated solution, you could simply use the Ext2 IFS for Windows, which works just fine with EXT3 partitions as well.
Much, much simpler.
http://www.fs-driver.org/
Usually ext2fsd is enough if i need to connect my hdd to another PC with Windows. Ubuntu is my main OS and Windows runs under VirtualBox. So this article is very interesting for sharing many other file systems except ext2/3, IMHO.
Or just install ifs drives in Windows. Seems a whole lot easier.
http://www.fs-driver.org/
I agree with Buzz.
http://www.chrysocome.net/explore2fs
I agree also, the above method is long, dangerous and not aligned with what a user wants, try below for a better option
http://www.ext2fsd.com/
If it only could support ex4….
@Arkadi, not sure which software/method you are referring to, but ext[3,4] are backwards compatible with ext2, so they should work fine. I have had no problems with ext3 and ext4 using ifsdrives in XP.
I think this is a good idea. I am sick and tired of loosing data with ext2fs, and having to reboot to linux to checkdisk each time the system crash.
To me, not the smarter way to access my data from an ext* partition.
Actually, since the amount of free space on the hard drive is no longer an issue, I’d rather prefer to sync everything on a NTFS partition, with native r/w support in win.
Hi ,)
How I can access from Windows to a ext4 partion ? Or must are have the partion ext3 ?
If you are running VirtualBox and have 64 bit capable CPU then you can run a 64 bit client on a 32 bit OS like Windows.
I would like to point out that this method may be long and difficult, but has the advantage that one can also mount filesystems that are stored in LVM, mdraid or dmraid, or through compression or encryption layers like encfs or cryptoloop. This is very helpful for people who dual-boot their systems, but does have the disadvantage of being more brittle. Here’s where a link to articles about the importance and facility of reasonable backup procedures would come in handy – but you already do backups from any platform you use, right? Me too!
heei, guys, any software suitable for windauz7?
What about ext4?
All:
You can mount ext4 ext3 and ext2 drives in windows with ifsdrive. It is THAT easy.
http://www.fs-driver.org/
Hi,
first of all thanks for interesting articke. It makes me to think about sharing seriously – Now I see Ubuntu files from Windows VirtualBox guest.
BTW, who is this tutorial for? Is it meant for people with dual boot? Why to have dual boot anyway, or why to install Windows directly to your hardware if you have Ubuntu installed already? It is far better to install Windows inside VirtualBox. VirtualBox supports “Shared Folders” – from manual: “allow you to access files of your host system (Ubuntu) from within the guest system (Windows)”.
In my case I am running Ubuntu 9.10 as main system, and Windows XP in VirtualBox just for must have windows only apps like CorelDraw (We are using Inscape as much as possible, but our customers are hooked).
This is my tutorial how to access Ubuntu user files (located on Ext4 partition) from Windows running in Virtual box on top of Ubuntu.
1) Install “VirtualBox Guest Additions” into Windows guest
2) Create dir called for example “Shared” in Nautilus
3) Right click on that folder and select “Sharing options”, check all options
4) Start Virtual Box manager, open settings for Windows virtual host (which has be powered off), go to Shared Folders and create one for your “Shared” dir.
5) Start Windows machine. Go do Explorer and add network drive.
Hope it helps somebody. Cheers 🙂
My first reaction was “there’s a driver for this” then I realised, “wait, you were looking specifically for a way to let a windows install see a 4TB linux software raid5 array. There’s no driver for *that*.”
This is a cunning workaround – thank you!
G
for ext4 and LVM you can also use http://ext2read.sf.net
Great article, really promissing !
Easy, simple and probably the most secure process.
Thanks for the Author and Martin Bajer comment.
+ Promissing alternative:
– [2010/06] http://sourceforge.net/projects/ext2read/files/
+ Otherwise:
– [2009/07] http://www.ext2fsd.com
http://sourceforge.net/projects/ext2fsd/files/
+ Alternatives :
– http://www.fs-driver.org
– http://www.chrysocome.net/explore2fs
– http://www.diskinternals.com/linux-reader/
However, please read carefully Feature, FAQ, LIMITATION, RISK, of each method.
Great article, Thanks
I’m glad I ran across this article since there were problems (sometimes severe) in the way Ext3 access worked in all the other solutions on my Windows 7 x64 installation.
Problem #1: about half of the “easier” solutions presented are read-only, so you cannot write to the Ext3 file system. Writing to the file system was a requirement for my use.
Problem #2: If you have a new installation of Ubuntu and used default settings for Ext3 then you cannot use ext2ifs since “Inodes that are larger than 128 bytes are not supported.” The default for new Ubuntu installs is 256 bytes.
Problem #3: As far as I can tell, that only leaves ext2fsd. It seems some people have gotten it working, but on my install it would only show the directories at the root level of my volume and showed no files inside any of them. This is after following all the alternate things people said to try like running it in compatibility mode for Windows Vista.
This left me no simpler solutions than using VirtualBox and it worked perfectly.
While it might be like using a hammer to crack a nut, at least it worked. Better for my situation than using a defective plastic spork that breaks every time you use it. It worked, which is more than I can say for all the other “easier” solutions.
Thanks for this awesome guide. It is the only way I could use a nice file backup filesystem like ext4 (I know there may be better ones for backup but I am not that into it) and still access it from Windows 7 64 bit.
i wanted to follow your guide – only that I dont have the raid volume before installing ubuntu.
Therefore I created a single primary partition in windows – then added the drives to virtualbox ..
only problem is : after installing ubunto to one of the vbox-drives (during installation it shows me all 5 vbox-drives) and booting up – i dont see any other drives aside /dev/sda which is no other than the primary vbox-drive where I installed ubuntu. I tried fdisk -l but it also only shows
/dev/sda with partition /dev/sda1 and lshw -C shows me /dev/sda and my cdrom . So .. Where are the other drives that are “there” according to virtualbox (they are present in the virtual machine devices… ) and how can i make them usable for mdadm and so on ?
WOW! thanks!!!
this is in my opinion one of the best solutions to acces/convert EXT3 files to NTFS using the SAMBA interface in combination with this nice tutorial, which does great job. All other solutions like Ext2 IFS, ext2explore always cause DATA LOSS, only your solution is the most clean one!
Presumably doing this will result in respectably fast read/write speeds?
Trying any of the in Windows read drivers or applications results in abysmally slow speeds in my experience.
Have tried using them to access content from Humax PVR devices but it’s unworkable due to the slow access speeds. Booting from a USB Ubuntu flash drive enable me to copy at full speed but means rebooting the machine and only performing that one task at the time